Norm：简单介绍如何衡量机器学习中向量的「大小」

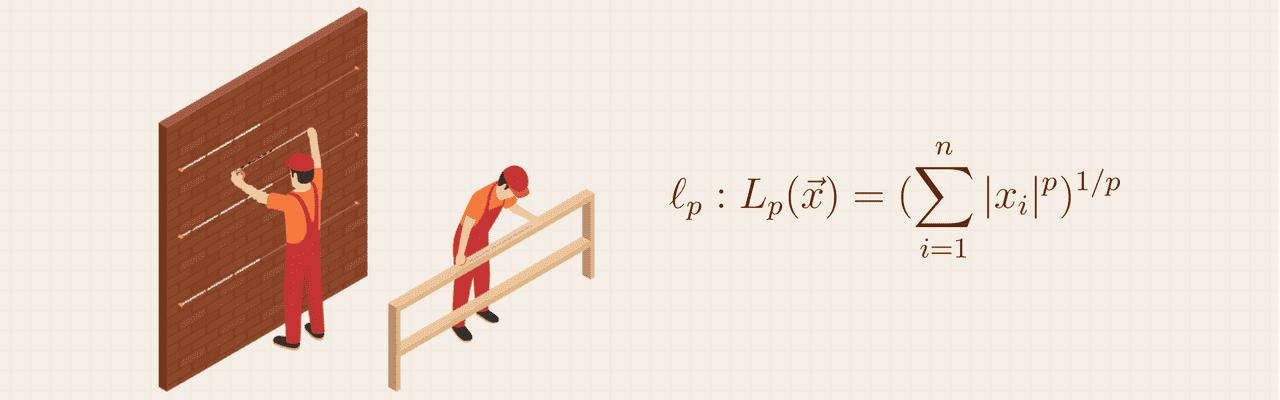
定量的衡量一个向量的长度或者大小往往是机器学习向量运算、矩阵运算中非常必要的一个任务，我们往往将「向量的长度」称为向量的范数：Vector's Norm。

范数（norm）：是具有「长度」概念的函数。在线性代数、泛函分析及相关的数学领域，是一个函数，其为向量空间内的所有向量赋予非零的正长度或大小。¹

最近，我在对抗样本攻击的研究中，需要定量的衡量「对抗样本」和「原图」之间的「扰动大小」。事实上，在机器学习里，不论是「对抗样本」还是其他的图片，它们本质上都可以用向量来表示，在 Python 中使用 Numpy 矩阵来存储和运算。这篇文章简单介绍（记录）一下一些 $\ell_p$ 范数的计算方法以及代码实现。

$\ell_p$ 范数

$\ell_p$ 范数实际上是向量空间中的「一组范数」²。在我的研究方向上，$\ell_p$ 范数也经常用于定量的衡量对抗样本的「扰动」幅度。我们将 $\ell_p$ 范数定义如下：

其中，$p$ 的取值可以是：$1$、$2$ 以及 $\infty$ 等，分别表示 $\ell_1$ 范数、$\ell_2$ 范数以及 $\ell_{\infty}$ 范数。

$\ell_0$ 范数

严格意义上来说，$\ell_0$ 范数并不是「范数」（所以定义中 $1/p$ 的 $p$ 也不能取值为 0），它表示的是向量中非零元素的个数。那么在对抗样本中，$\ell_0$ 范数表示的就是「扰动」中非零元素的个数。

$\ell_1$ 范数

$\ell_1$ 范数表示的是向量空间中所有向量长度之和，一个比较形象的形容就是：在向量空间中，你需要从一个向量的起点走到另一个向量的终点，那么你行程的距离（经过向量的总长度）就是向量的 $\ell_1$ 范数。

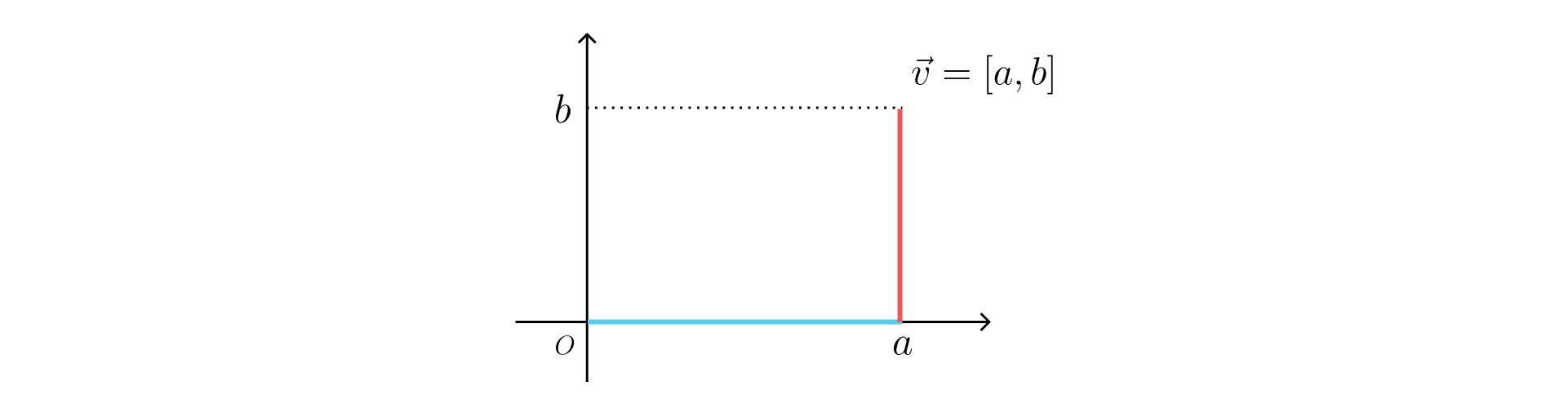
如上图，$\ell_1$ 即可以按照下式计算得到：

就像出租车（Taxicab）沿着路线行驶全程所经过的距离。因而，$\ell_1$ 范数也被称为 Taxicab 范数或者 Manhattan 范数。（因为曼哈顿的街道大部分都是矩形直角分布的！🤣）

$\ell_2$ 范数

$\ell_2$ 范数是机器学习领域更为常用的一种向量大小的衡量方法。$\ell_2$ 范数也被称为欧式范数（Euclidean norm），表示的是从一点到另一点所需的最短距离。

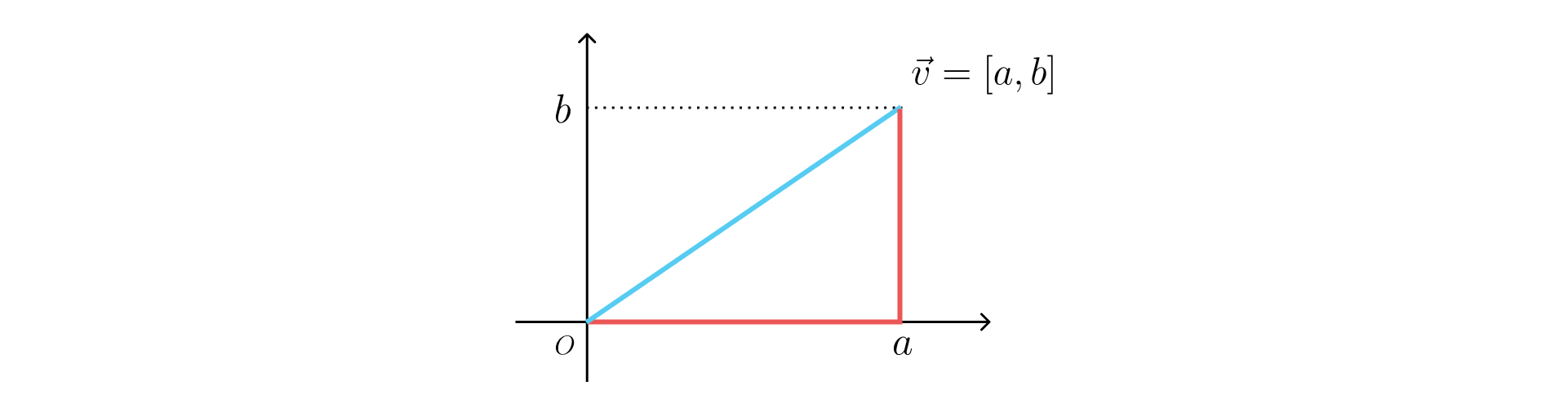
按照如上图所示的例子，$\ell_2$ 范数就是按照下式进行计算得到的：

$\ell_\infty$ 范数

$\ell_\infty$ 范数理解起来就非常简单，即为向量元素里面绝对值最大的元素的长度（大小）：

比如给定一个向量 $\vec{v}=[-10,3,5]$，那么向量的 $\ell_\infty$ 范数就是 $10$。

代码实现

在我的研究中，我往往使用 $\ell_p$ 范数衡量对抗样本的扰动大小。很遗憾，我所使用的 Foolbox 框架并没有直接给出所有 $\ell_p$ 范数计算的距离值（distance），所有我往往需要用 Numpy 进行计算。

对于一个图片 img，以及其对抗样本 adv，我们可以轻松的计算得到「扰动」perturb：

# perturb is a numpy array
perturb = adv - img

那么，我们就可以使用 Numpy 来计算扰动 perturb 的各项 $\ell_p$ 范数：

# import numpy and relevant libraries
import numpy as np
from numpy.linalg import norm

# L0
_l0 = norm(perturb, 0)
# L1
_l1 = norm(perturb, 1)
# L2
_l2 = norm(perturb)
# L∞
_linf = norm(perturb, np.inf)

事实上，numpy.linalg.norm 的内部实现中，就是利用 $\ell_p$ 的定义进行的向量运算。比如 $\ell_1(x)$ 就是：

_l1_x = np.sum(np.abs(x))

$\ell_\infty(x)$ 就是：

_linf_x = np.max(np.abs(x))

等等（上面是对于向量来说的两种简单算法，没有考虑特殊情况，生产环境中尽量使用 numpy.linalg.norm 提供的方法）。在 Numpy 的官方文档中，Numpy 也给出了 $\ell_p$ 范数在矩阵和向量不同情况下的计算方法。

延伸阅读

• Numpy 文档 - numpy.linalg.norm
• Medium - L0 Norm, L1 Norm, L2 Norm & L-Infinity Norm
• Gentle Introduction to Vector Norms in Machine Learning